How To Convert Odds To Probability
Convert Decimal Odds into Probability. If we use the decimal odds of 1.80 for this and use the following equation:. 1 / decimal odds x 100 = implied probability. So, 1 / 1.80 is 0.555 (rounded up to 0.56), giving the mathematical equation of 0.56 x 100 = 56%. This means that odds of 1.80 reflect a 56% chance of that particular outcome. If odds are stated as an A to B chance of winning then the probability of winning is given as P W = A / (A + B) while the probability of losing is given as P L = B / (A + B). For example, you win a game if you pull an ace out of a full deck of 52 cards. Pulling any other card you lose.
- How To Convert Odds To Probability
- How To Change Odds To Probability
- How Do You Convert Odds To Probability
- How To Convert Betting Odds Into Probability
- How To Convert Odds To Probability
- Converting Betting Odds To Probability
To convert odds to probability, add the successes and failures to find the total. Then divide the number of successes by the total to calculate the probability. Example: Suppose the odds of a casino game are 2:3. Since 2+3 = 5 we take 5 as the total. Thus the probability is 2/5 = 0.4 = 40%. In order to convert decimal odds to the implied probability, a simple formula of 1 divided by the odds and then multiplied by 100 gives the expected outcome. Essentially, I'd like to see if I can provide insight into how much the probability is influenced by each feature. To do this, I used the following formula: 1 + 1 / exp (-logodd) and I would expect that after I convert all of the explanations for a specific prediction to probabilities, the sum should be zero.
Here is a fairly simple question with an equally simple and straightforward answer. How does one convert the odds ratio to the probability of winning in sports handicapping. Crazy as it sounds, this question was right up my high school baseball coach’s alley, as he was also my teacher in probability and statistics (some fun school class I had back in the day). And yes, I did just put fun and school in the same sentence. And no, I wasn’t being sarcastic. He always made baseball fun, whether at practice, driving on a bus to an away game, or in the game itself. And his class was fun as well (at least for me). No idea if he handicapped sports, or if he ever ran equations in his head any time he flashed the bunt or steal sign. Anyway, without further ado…
Flipping a Coin – What are odds?
So, we all probably have no doubt that a coin flip would result in 50% chance of heads and 50% chance of tails. The coin only has two sides. So here, we simple divide our desired outcome (1) by the two possible outcomes (2) and multiply by 100 to give us our answer in a percentage.
1 / 2 x 100


.5 * 100 = 50%
A roll of a die (or singular form of dice)
Die or dice, whatever you want to call the singular form of dice. We have one. It has 6 sides, what is the probability that we get a 3 from rolling it? Well, to answer this, we take the 1 desired result (the 3) and divide it by 6 (the 6 possible outcomes). Then we multiply the answer by 100 to put our answer in percentage form.
1 / 6 * 100
.1667 * 100 = 16.67%
Here, we have a 16.67% chance of rolling our desired outcome.
Advertisement for zcodesystem.com
Types of Odds
The most common forms of odds used today are decimal odds, fractional odds and American odds (the moneyline). We will go through each below. First, however, why is this important? Well, by converting the betting odds into something often referred to as implied probability, we can better access the value of a particular market. Do they differ from what we believe the odds of winning should be? If the odds offered to us (the implied probability) are less than or greater than our personal assessment, then this would represent either an increase or decrease in betting value.
Decimal Odds – How to Convert Odds Ratio to Probability in Sports Handicapping
First on the above list, are the decimal odds. These odds are common in Europe. The decimal odds represent the amount that is won for every $1 wagered. Say for example the odds are represented as 2.5, this would imply that for every 1 you wager, you will gain a profit of 1.5 if the outcome was in your favor. Here, to convert odds ratio to probability in sports handicapping, we would have the following equation:
(1 / the decimal odds) * 100
or
How To Convert Odds To Probability
(1 / 2.5) * 100
Quickly, doing the math in my head (kidding, I used a calculator), the answer is 40%
Fractional Odds – How to Convert Odds Ratio to Probability in Sports Handicapping
When I think of the odds represented in a fractional format, I automatically think of horse racing. Let’s say the odds of Aggressive Neil to win are represented as 9 / 2, how do we translate? Well the equation is as follows:
Denominator / (Denominator + Numerator) * 100
Or with our 9 /2 example:
2 / (2 +9) *100
Using my overused calculator, I get an 18.18% chance of winning.
American Odds (The Moneyline) – How to Convert Odds Ratio to Probability in Sports Handicapping
Used much in North America for sports such as baseball, basketball, hockey and others, the moneyline is actually not as confusing as one would first think. Each game or match will have teams with either a plus moneyline or a minus moneyline. A +180 for example would imply that for every $100 wagered the winnings would be $180 gross or $80 net. So, the plus moneyline would represent the underdog for the game or match.
Conversely, a -180 line essentially means the team is the favorite to win, and to win $100, one would need to wager $180. So, here, how do we convert these odds into the probability of winning in sports handicapping?
Well, in the case of the moneyline, we have the following equation for the plus moneyline:
100 / (plus moneyline +100) * 100 (to put it as a percentage)
Or using the example above,
100 / (180 + 100) *100
Here my calculator gives me a 35.71% chance of winning.
And for the minus moneyline, I basically use the absolute value or (in my simple terms) remove the negative sign in the value. The calculation for chance of winning would then look something like this:
(absolute value of negative line odds) / (absolute value of negative line odds + 100)* 100 (to put it as a percentage)
Or using above example:
How To Change Odds To Probability
180 / (180 +100) *100
And, here, my calculator throws out a 64.29% chance of winning.
Places Online to Convert the Odds Ratio to Probability in Sports Handicapping
Ok, so maybe I should have blurted out the following websites right up front. But now, we at least understand the formulas used to convert the odds ratio to probability in sports handicapping. One webpage I found that calculates these odds into a percentage is from aceodds.com. Here is the link.
Another webpage, I found is from actionnetwork.com. Here is the link.
Moneyline (American Odds) to Percentage Conversion Chart
I personally like the online calculators mentioned above for our topic and mission here. However, you may want a spreadsheet version of the calculations instead. If this describes you, I’ll throw a quick moneyline to percentage conversion chart at the end of this article.
Why Do the Odds that Bookmakers Give You Not Add Up to 100%
So, why is it that the odds that bookmakers offer do not equate to 100% when combined? For example, in major league baseball, let’s say the Seattle Mariners are visiting the Oakland Athletics today. The odds may have the game at Seattle Mariners +120 and Oakland Athletics -130. Do the above equations and we come up with the Seattle Mariners percentage value of 45.45% and the Oakland Athletics percentage value of 56.52%. Add the two and we come up with a total percentage value of 101.97%. What is with this figure? Well, that 1.97% is the bookmakers edge incorporated into the odds, their expected return for setting up the bet.
Why Do the Odds Move Throughout the Day?
So, you probably have noticed the lines moving throughout the day. These lines are not static? In our Seattle Mariners vs. Oakland Athletics game above (which I did grab from a past game played), we again have the odds listed at Seattle Mariners +120 and Oakland Athletics -130. These were not, however, the odds the game opened at. The opening odds were actually Seattle Mariners +107 and Oakland Athletics -127. So, why did this particular sportsbook move the line from +107 to +120 and -127 to -130? Well, most likely the lines moved to entice more action to the Seattle Mariners. The sportsbook wants to “balance the books”, and they will move the lines one way or the other to entice more action to one side of the equation.
In Summary
Hey, sportsbooks are around to make money for themselves. The lines may fluctuate throughout the course of the day in an attempt to match the bets as close to 50% one side and 50% the other. The left over percentage that we described above is how the books make money. Let’s say your assessed probability is of a greater percentage than that of the bookmaker’s implied probability. This creates an opportunity, a value betting opportunity.
And below is the a table of the moneyline to percentage conversion chart mentioned above.
| Moneyline | Probability | Moneyline | Probability |
| 350 | 22.2% | -350 | 77.8% |
| 345 | 22.5% | -345 | 77.5% |
| 340 | 22.7% | -340 | 77.3% |
| 335 | 23.0% | -335 | 77.0% |
| 330 | 23.3% | -330 | 76.7% |
| 325 | 23.5% | -325 | 76.5% |
| 320 | 23.8% | -320 | 76.2% |
| 315 | 24.1% | -315 | 75.9% |
| 310 | 24.4% | -310 | 75.6% |
| 305 | 24.7% | -305 | 75.3% |
| 300 | 25.0% | -300 | 75.0% |
| 295 | 25.3% | -295 | 74.7% |
| 290 | 25.6% | -290 | 74.4% |
| 285 | 26.0% | -285 | 74.0% |
| 280 | 26.3% | -280 | 73.7% |
| 275 | 25.7% | -275 | 74.3% |
| 270 | 27.0% | -270 | 73.0% |
| 265 | 27.4% | -265 | 72.6% |
| 260 | 27.8% | -260 | 72.2% |
| 255 | 28.2% | -255 | 71.8% |
| 250 | 28.6% | -250 | 71.4% |
| 245 | 29.0% | -245 | 71.0% |
| 240 | 29.4% | -240 | 70.6% |
| 235 | 29.9% | -235 | 70.1% |
| 230 | 30.3% | -230 | 69.7% |
| 225 | 30.8% | -225 | 69.2% |
| 220 | 31.3% | -220 | 68.7% |
| 215 | 31.7% | -215 | 68.3% |
| 210 | 32.3% | -210 | 67.7% |
| 205 | 32.8% | -205 | 67.2% |
| 200 | 33.3% | -200 | 66.7% |
| 195 | 33.9% | -195 | 66.1% |
| 190 | 34.5% | -190 | 65.5% |
| 185 | 35.1% | -185 | 64.9% |
| 180 | 35.7% | -180 | 64.3% |
| 175 | 36.4% | -175 | 63.6% |
| 170 | 37.0% | -170 | 63.0% |
| 165 | 37.7% | -165 | 62.3% |
| 160 | 38.5% | -160 | 61.5% |
| 155 | 39.2% | -155 | 60.8% |
| 150 | 40.0% | -150 | 60.0% |
| 145 | 40.8% | -145 | 59.2% |
| 140 | 41.7% | -140 | 58.3% |
| 135 | 42.6% | -135 | 57.4% |
| 130 | 43.5% | -130 | 56.5% |
| 125 | 44.4% | -125 | 55.6% |
| 120 | 45.5% | -120 | 54.5% |
| 115 | 46.5% | -115 | 53.5% |
| 110 | 47.6% | -110 | 52.4% |
| 105 | 48.8% | -105 | 51.2% |
| 100 | 50.0% | 100 | 50.0% |
Logistic regression may give a headache initially. While the structure and idea is the same as “normal” regression, the interpretation of the b’s (ie., the regression coefficients) can be more challenging.
This post provides a convenience function for converting the output of the glm function to a probability. Or more generally, to convert logits (that’s what spit out by glm) to a probabilty.
Note1: The objective of this post is to explain the mechanics of logits. There are more convenient tools out there. (Thanks to Jack’s comment who made me adding this note.)
Note2: I have corrected an error pointed out by Jana’s comment, below (you can always check older versions on the Github repo).
So, let’s look at an example. First load some data (package need be installed!):
Compute a simple glm:
How Do You Convert Odds To Probability
The coeffients are the interesting thing:
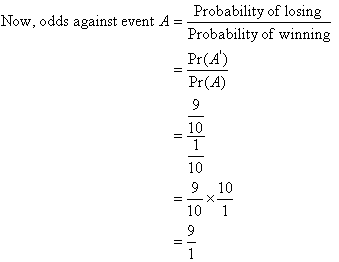

These coefficients are in a form called ‘logits’.
If coefficient (logit) is positive, the effect of this predictor (on survival rate) is positive and vice versa.
Here Pclass coefficient is negative indicating that the higherPclass the lower is the probability of survival.
To convert a logit (glm output) to probability, follow these 3 steps:
- Take
glmoutput coefficient (logit) - compute e-function on the logit using
exp()“de-logarithimize” (you’ll get odds then) - convert odds to probability using this formula
prob = odds / (1 + odds). For example, sayodds = 2/1, then probability is2 / (1+2)= 2 / 3(~.67)
This function converts logits to probability.
For convenience, you can source the function like this:
For our glm:
How to interpret:
- The survival probability is 0.8095038 if
Pclasswere zero (intercept). - However, you cannot just add the probability of, say
Pclass 1to survival probability ofPClass 0to get the survival chance of 1st class passengers.
Instead, consider that the logistic regression can be interpreted as a normal regression as long as you use logits. So the general regression formula applies as always:
That is, in our example
where b_survival is given in logits (it’s just the b-coefficient of Pclass).
So, it’ simple to calculate by hand, eg., the survival logits for a 2nd class passenger:
Thus, the logits of survival are -0.25Now we can convert to probability:
Remember that (e^1 approx 2.71). That is, if your logit is 1, your odds will be approx. 2.7 to 1, so the the probability is 2.7 / 3.7, or about 3/4, 75%.
Similarly important, (e^0 = 1). Hence, your odds will be 1:1, ie., 50%.
Hence, whenever your logit is negative, the associated probability is below 50% and v.v. (positive logit <–> probability above 50%).
However, more convenient would be to use the predict function instance of glm; this post is aimed at explaining the idea. In practice, rather use:
How To Convert Betting Odds Into Probability
In the 1st class, survival chance is ~65%, and for 2nd class about 44%.
How To Convert Odds To Probability
Here’s a look up table for the conversion:
| Logit | Probability | |
|---|---|---|
| 1 | -10 | 0 |
| 2 | -8 | 0 |
| 3 | -6 | 0.002 |
| 4 | -4 | 0.018 |
| 5 | -2 | 0.119 |
| 6 | 0 | 0.5 |
| 7 | 2 | 0.881 |
| 8 | 4 | 0.982 |
| 9 | 6 | 0.998 |
| 10 | 8 | 1 |
| 11 | 10 | 1 |
A handy function is datatable, does not work in this environment however it appears.
The package mfx provides a convenient functions to get odds out of a logistic regression (Thanks for Henry Cann’s comment for pointing that out!).
More convenient for an overview is a plot like this.
The relationship between logit and probability is not linear, but of s-curve type.
The coefficients in logit form can be be treated as in normal regression in terms of computing the y-value.
Converting Betting Odds To Probability
Transform the logit of your y-value to probability to get a sense of the probability of the modeled event.
Happy glming!